I've been playing around with polynomials recently. One thing struck me about the association between the roots of a polynomial and its coefficients. As you know, the coefficients of a monic polynomial of degree @@n@@ are completely determined by its set of @@n@@ roots. So, we can map vectors of roots @@\begin{pmatrix} r_1 & \cdots & r_n \end{pmatrix}^\intercal \in \CC^n@@ to their vectors of coefficients @@\begin{pmatrix} c_0 & \cdots & c_{n-1} \end{pmatrix}^\intercal \in \CC^n@@ via

%% \begin{align*} p(x) &= x^n + c_{n-1} x^{n-1} + \cdots + c_1 x + c_0 \nl &= (x-r_1) \cdot \cdots \cdot (x-r_n). \end{align*} %%

Let's call this function @@\mathcal{V} : \CC^n \to \CC^n@@. Now, @@\mathcal{V}@@ is continuous — in fact it's holomorphic, as can be seen by just expanding the product and looking at the resulting coefficients. Furthermore, the inverse is "locally continuous". That's not the technical term; I invented it. What I mean is that if @@\mathcal{V}(\mathbf{r}) = \mathbf{c}@@, then for any small perturbation to @@\mathbf{c}@@ called @@\mathbf{c}^\prime@@, I can find a small perturbation to @@\mathbf{r}@@ called @@\mathbf{r}^\prime@@ such that @@\mathcal{V}(\mathbf{r}^\prime) = \mathbf{c}^\prime@@. I didn't prove this; I just intuited it by Taylor-expanding polynomial in question about each root.

Apparently, this map has a name; @@\mathcal{V}@@ is the Viète map. That name comes from this StackExchange thread. It mainly looks at showing the statement from the last paragraph — that the roots of a polynomial locally depend continuously on its coefficients. Turns out, it's not obvious how to prove that. My intuition works for square-free polynomials, and this Wikipedia page says that the holomorphic implicit function theorem gives the required result in that case. I also like the proof given by Alexandrian,¹ since it uses complex analysis rather than topology.

Regardless, I think another way to state my observation is: the set @@\CC^n@@ covers itself multiple times.² In fact, it @@n!@@-covers itself, since every permutation of the roots maps to the same sequence of coefficients. I'm not entirely sure why, but this was surprising to me. In the context of sets, there are things like Hilbert's Hotel and Banach–Tarski. The latter is more relevant here, since (one formulation of) it shows that @@S^2@@ can "map over" itself twice. Neither of these examples use continuous functions though, and I thought enforcing continuity would prevent this from happening. Obviously, not the case.

This isn't even the simplest example of multiple-covering I can think of. The circle @@S^1 \cong \RR / 2\pi\ZZ@@ covers itself any number of times. For any positive integer @@k@@, simply do @@t \mapsto k \cdot t@@. In a similar vein, the punctured complex plane @@\CC \setminus \{0\}@@ @@k@@-covers itself via the map @@z \mapsto z^k@@.

---

I started wondering if I could use @@\RR@@ to cover itself exactly @@k@@ times, for any positive number @@k@@. At first, I considered a weaker condition:³

Definition: I'll say that a continuous function @@f: X \to Y@@ @@k@@-hits @@Y@@ if, for every @@y@@, there are exactly @@k@@ distinct @@x@@ such that @@f(x) = y@@. If @@k \geq 2@@, then I'll say that @@f@@ multiple-hits @@Y@@.

I make this definition by analogy to covering. It drops the requirement that @@f@@ locally be a homeomorphism, meaning it also doesn't have to have a locally continuous inverse.

At first, I thought it was impossible to multiple-hit @@\mathbb{R}@@ from @@\mathbb{R}@@ itself. Polynomials have been on my mind recently, and indeed it is impossible for polynomials.

Observation: For any polynomial @@p : \RR \to \RR@@, there is some infinite interval @@I@@ containing points such that, for any @@y \in I@@, @@p(x) = y@@ has at most one solution.

First note that @@p@@ will eventually become monotonic as @@x \to \pm \infty@@. So let @@p@@ be monotonic on @@L := (-\infty, x_\min)@@ and on @@R := (x_\max, \infty)@@. The polynomial @@p@@ need not have the same "tonicity" on @@L@@ and @@R@@; it could be monotonically increasing on one and monotonically decreasing on the other. Regardless, the extreme value theorem gives that, on the interval @@M := [x_\min, x_\max]@@, @@p@@ attains a minimum and maximum @@y_\min@@ and @@y_\max@@ respectively.

Now consider two candidate intervals @@I_- = (-\infty, y_\min)@@ and @@I_+ = (y_\max, \infty)@@. By construction, no @@x \in M@@ can cause @@p@@ to evaluate to a @@y \in I_- \cup I_+@@, so any solutions there must come from @@L@@ or @@R@@. Using the monotonicity of @@p@@ and the fact that

%% y_\min \leq p(x_\min) = p(x_\max) < y_\max, %%

we see that in fact each of @@L@@ and @@R@@ contribute at most one solution to @@y@@s in either @@I_-@@ or @@I_+@@ (but not both). Doing casework, we can choose one of those intervals to be the returned result. □

This observation can be made even stronger: if some @@y \in I@@ has a solution, then all of them do. That can be shown by using the fact @@\lim_{x \to \pm \infty} p(x) = \pm \infty@@.

So polynomials are not enough. Still, the technique of "sign analysis", which I originally learned for polynomials,⁴ can sometimes be applied to continuous functions.

Definition: Let @@f@@ by a continuous function such that @@f(x) = y@@ has finitely many solutions @@x_1, \cdots, x_k@@. I define the sign chain of @@f@@ at @@y@@, which I denote @@\chn{f}{y}@@, as the list of length @@k+1@@ containing whether @@f@@ is greater than (@@+@@) or less than (@@-@@) @@y@@ on the subintervals @@(-\infty, x_1)@@, @@(x_1, x_2)@@, …, @@(x_k, \infty)@@.

So for example, consider the function @@x^3 - x@@. Its sign chain at @@y = 0@@ is @@[-, +, -, +]@@, while at @@y = 1@@ it's @@[-, +]@@. Note that the sign chain doesn't have to alternate. Consider @@\chn{x^2}{0} = [+, +]@@.

This notion is well-defined. No subinterval can contain an @@x@@ where @@f(x) = y@@. If one does, we missed a solution. Furthermore, no subinterval can contain @@x_a, x_b@@ such that @@f(x_a) < y@@ and @@f(x_b) > y@@ or vice versa. If one does, then the intermediate value theorem can find a solution we missed.

Definition: If @@c@@ is a sign chain, I define the sign of that sign chain, which I denote @@\sgn{c}@@, as even (@@+1@@) if consecutive elements of @@c@@ differ an even number of times, and odd (@@-1@@) otherwise. Equivalently, @@\sgn{c}@@ is even if the first and last elements of @@c@@ are the same, and odd if they are different.

So for example, @@\sgn{[-, +, -, +]} = -1@@, while @@\sgn{[+, +]} = +1@@.

Usually, we were interested in sign chains of polynomials at zero. Those are particularly helpful for plotting, and they have some nice properties. For example, the sign of any sign chain for any polynomial concides with the parity of that polynomial's degree, and the sign difference between consecutive elements of the sign chain at zero gives the parity of the multiplicity of the corresponding root.

Returning to our original goal of multiple-hitting @@\RR@@ though, we have the following.

Lemma: Let @@f : \RR \to \RR@@ be a surjective continuous function, and let @@f(x) = y@@ have only finitely many solutions @@x_1, \cdots, x_k@@ for some @@y@@. Then, @@\sgn{\chn{f}{y}} = -1@@.

We'll prove the contrapositive. Assume @@\sgn{\chn{f}{y}} = +1@@, and without loss of generality assume the first entry in @@\chn{f}{y}@@ is a @@+@@. Then the last entry is also a @@+@@ due to the sign of the sign chain. Ultimately @@f(x) > y@@ when @@x \in (-\infty, x_1) \cup (x_k, \infty)@@. Furthermore, the extreme value theorem bounds @@f(x) \in [y_\min, y_\max]@@ when @@x \in [x_1, x_k]@@. Note that, @@y \geq y_\min@@ since @@y = f(x_1)@@ and @@y = f(x_k)@@ by definition. No matter where @@x@@ is located, we have that @@f(x) \geq y_\min@@, so @@f@@ cannot be surjective. □

Theorem: If @@f : \RR \to \RR@@ @@k@@-hits, then @@k@@ is odd.

Start by picking any @@y@@. Let @@x_1, \cdots, x_k@@ be the solutions to @@f(x) = y@@, and let @@c = \chn{f}{y}@@. Now we'll consider offsetting @@y@@ by a small amount. For now, we'll consider shifting it up to @@y + \epsilon@@. If we do this, every subinterval @@(x_i, x_{i+1})@@ of @@c@@ where @@f(x) > y@@ — every "interior" @@+@@ subinterval — gives at least two solutions to @@f(x) = y + \epsilon@@. To see this, choose @@\epsilon@@ small enough that

%% f(x_i), f(x_{i+1}) = y < y + \epsilon < \max_{x \in (x_i, x_{i+1})} f(x). %%

⁵ The intermediate value theorem gives at least two crossing points: one on the way up to the maximum from @@f(x_i)@@, and one on the way back down from the maximum to @@f(x_{i+1})@@.

Now for the "exterior" subintervals. Due to the previous lemma, exactly one of those two subintervals of @@c@@ — either @@(-\infty, x_1)@@ or @@(x_k, \infty)@@ — is @@+@@ and thus has @@f(x) > y@@. Without loss of generality, let's say its the left one. This subinterval gives at least one solution to @@f(x) = y + \epsilon@@. Again, choose any @@\epsilon@@ small enough that

%% f(x_1) = y < y + \epsilon < \sup_{x \in (-\infty, x_1)} f(x). %%

⁶ If we do that, we have @@f(x) > y + \epsilon@@ for some @@x \in (-\infty, x_1)@@, at which point the intermediate value theorem gives a point with equality.

In the end, if @@n_+@@ is the number of @@+@@ intervals in @@c@@, then @@f(x) = y + \epsilon@@ has at least @@2n_+ - 1@@ solutions. The @@n_+ - 1@@ interior subintervals contribute at least two solutions each, and the one exterior subinterval gives at least one more. Now since @@f@@ @@k@@-hits @@\RR@@, we have

%% 2n_+ - 1 \leq k. %%

We considered shifting @@y@@ up by a small amount here, but we could've shifted it down by a small amount. Doing analogous steps gives

%% 2n_- - 1 \leq k. %%

And of course, every subinterval is either @@+@@ or @@-@@, so @@n_+ + n_- = k + 1@@, which is the length of the whole list @@c@@.

Now, algebra. We can sum the two inequalities to find that

%% 2n_+ + 2n_- \leq k + 2. %%

But doubling the equality constraint gives

%% 2n_+ + 2n_- = k + 2. %%

The only way for this to work is for both the inequalities to be tight. In other words,

%% \begin{align*} n_+,n_- &= \frac{k+1}{2}. \end{align*} %%

Since @@n_+@@ and @@n_-@@ are both integers, this only works if @@k@@ is odd. □

(I really hope this proof is correct. I don't fully understand how badly behaved continuous functions can be though!)

So that gives us some constraints on what multiple-hitting functions look like. But can we get a concrete example? I found this:

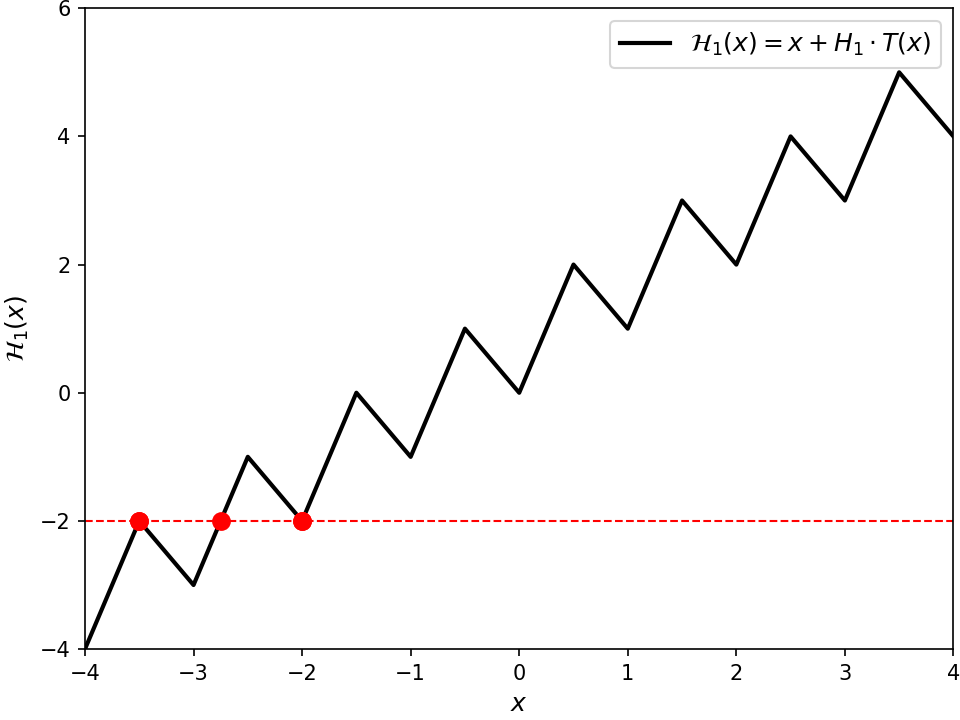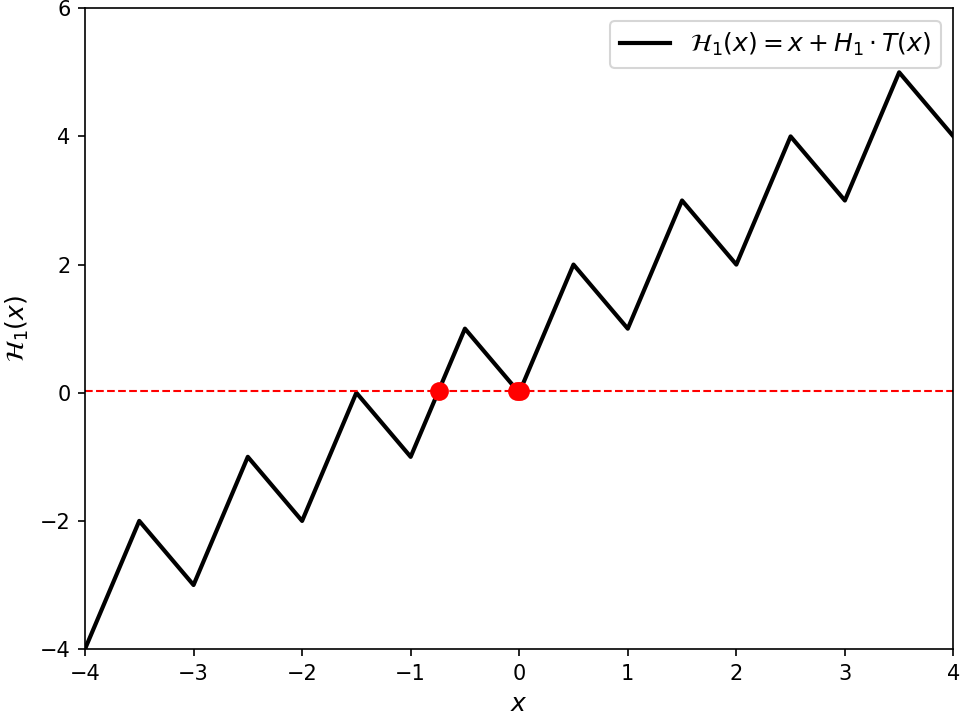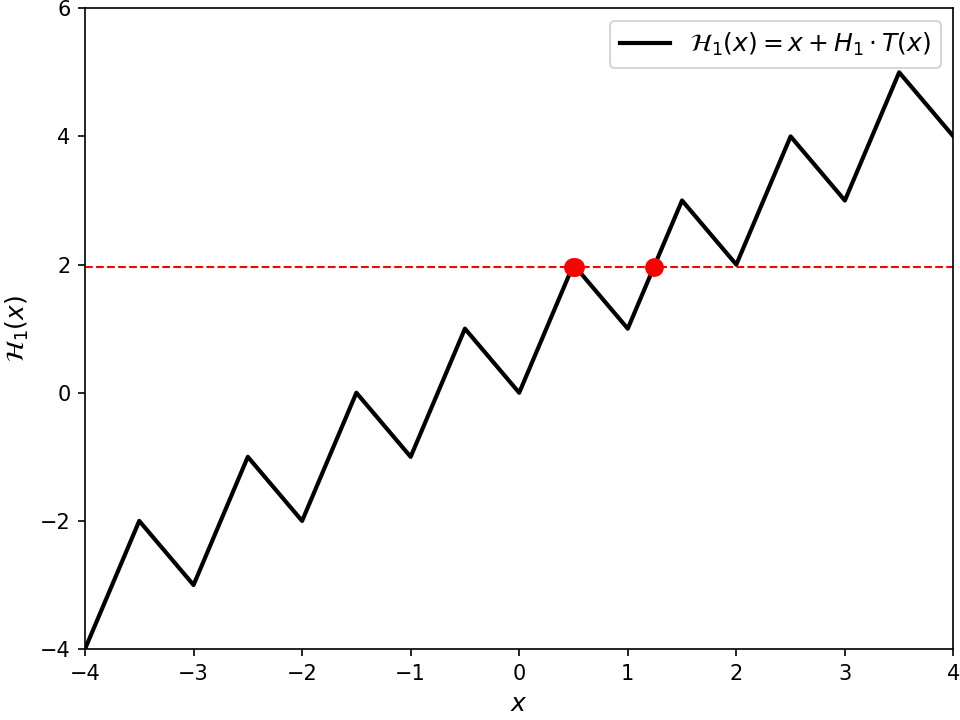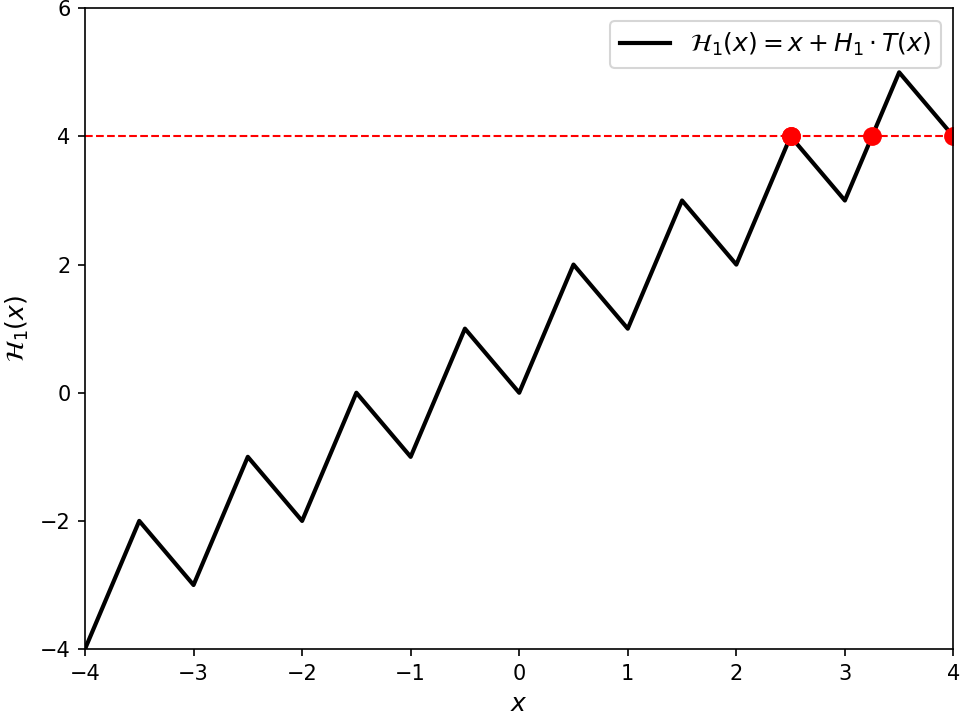
%% \mathcal{H}_1(x) = x + H_1 \cdot T(x), %%

where

%% T(x) = \begin{cases} \{x\} & \text{if } \{x\} \leq \frac{1}{2} \nl 1 - \{x\} & \text{if } \{x\} \geq \frac{1}{2} \end{cases}, %%

@@\{x\} = x - \lfloor x \rfloor@@ is the fractional part of the real number @@x@@, and @@H_1@@ happens to be @@3@@. The function @@T@@ is a triangle wave starting at zero with a period of one and spanning @@[0, \frac{1}{2}]@@. This function seems to @@3@@-hit @@\RR@@, as shown in the plot below. Sweeping up the @@y@@-axis, each "trough" creates a new solution which then splits into two. These two solutions go to the two adjacent "peaks", where they each merge with another solution, then annihilate. The scaling factor @@H_1@@ times it so that a solution pair is annihilated precisely when a new one is created, so overall the number of solutions always remains the same.

In general, it seems this framework can be used to create functions that @@(2t + 1)@@-hit @@\RR@@, for all positive integers @@t@@. Because of the theorem above, this framework gives examples of functions that @@k@@-hit @@\RR@@ for every possible value of @@k@@ (except for the trivial @@k = 1@@ case). We just set

%% H_t = 2t + 1. %%

I got that value by solving for when the trough at @@x = 0@@ is at the same height as the peak at @@x = -\frac{1}{2}(2t + 1)@@.

---

Even though these @@\mathcal{H}_t@@ functions multiple-hit @@\mathbb{R}@@, they don't multiple-cover @@\mathbb{R}@@ since their inverse isn't locally continuous. To see this, observe that at @@x = 0@@ the output is @@y = 0@@. But if nudge the output down slightly to @@y = -\epsilon@@, I can't make a small nudge to the input to acheive that output, since it's in the middle of a trough. I think this is fundamental:

Conjecture: No simply connected topological space admits a (non-trivial) multiple-covering.

This statement is actually true; see this StackExchange thread and this blog post. I just don't know the machinery to prove it, so I mark it as a conjecture.

If we require the covering space @@p : \tilde{X} \to X@@ to be path-connected, I think I want to do the following. Suppose @@x \in X@@ has two preimages @@\tilde{x}_0@@ and @@\tilde{x}_1@@. Let @@\tilde{\gamma}@@ be a path in @@\tilde{X}@@ between those two points. Under @@p@@, that path maps to a loop @@\gamma@@ in @@X@@. But since @@X@@ is simply connected, we can contract @@\gamma@@ to a point. I want to continuously deform @@\tilde{\gamma}@@ so that it always maps to @@\gamma@@ throughout the contraction.

In the end, @@\tilde{\gamma}@@ would be a path from @@\tilde{x}_0@@ to @@\tilde{x}_1@@, while @@\gamma@@ is constant at @@x@@. We'd get an entire continuous path of points mapping to the same point. And because @@p@@ is a covering, this would give a large family of open sets in @@\tilde{X}@@, each disjoint from each other, and each homeomorphic to a particular open set containing @@x@@. This is certainly weird. It should be possible to derive a contradiction from here, or at the very least to add more conditions to @@\tilde{X}@@ to cause a contradiction. □

At the very least, this conjecture is consistent with the datapoints we've collected so far. The circle @@S^1@@ and the nonzero complex numbers @@\CC \setminus \{0\}@@ both can be multiple-covered — by themselves in fact — and are both not simply connected. You may object, saying that the map that started this whole adventure @@\mathcal{V} : \CC^n \to \CC^n@@ is a counterexample. Unfortunately, I lied. The Viète map fails to be a covering space since, even though it is locally invertible, it is not uniquely locally invertible. If I have @@\mathcal{V}(\mathbf{c}) = \mathbf{r}@@, and I make a small adjustment to get @@\mathbf{r}^\prime@@, I may have multiple choices for @@\mathbf{c}^\prime@@. As an example, consider @@\mathbf{r} = x^2@@ and @@\mathbf{c} = (x-0)\cdot(x-0)@@. If I perturb @@\mathbf{r}^\prime = x^2 - \epsilon^2@@, then I can choose between @@\mathbf{c}^\prime = (x + \epsilon) \cdot (x - \epsilon)@@ or @@(x - \epsilon) \cdot (x + \epsilon)@@. Order matters here since we're viewing these as vectors.

We can restrict @@\mathcal{V}@@ by forcing its inputs to have distinct elements. In that case, it would map from the configuration space @@\Conf{\CC}{n}@@ to some subset of @@\CC^n@@. It wouldn't map to the whole space though, so it wouldn't constitute a multiple-cover. Still,

Theorem: Assuming @@n \geq 2@@, @@\Conf{\CC}{n}@@ is not simply connected.

Intuitively, we're starting with something that looks like a real vector space of dimension @@2n@@ and removing a finite number of subspaces of dimension @@2n - 2@@. This space is path connected because disconnecting @@\RR^{2n}@@ requires removing a subspace of dimension @@2n-1@@ or higher. It's not simply connected since we can create non-contractible loops by wrapping a path, occupying a two-dimensional plane, around one of the subspaces we removed.

Formally, I'll just show that there exist non-contractible loops in @@\Conf{\CC}{n}@@.⁷ Suppose for the sake of contradiction that the path

%% \gamma(t) = \begin{pmatrix} e^{2\pi i \cdot t} & -e^{2\pi i \cdot t} & z_3 & \cdots & z_n \end{pmatrix}^\intercal %%

is contractible to a point. It doesn't matter what the higher components @@z_3, \cdots, z_n@@ are exactly, as long as they are distinct and don't lie on the unit circle. Now look at the function

%% f(\mathbf{z}) = z_1 - z_2 %%

that subtracts the first two components of the supplied vector. If the domain of @@f@@ is taken to be @@\Conf{\CC}{n}@@, then the range of @@f@@ is the punctured complex plane @@\CC \setminus \{0\}@@ because @@z_1 \neq z_2@@.

Now, @@f \circ \gamma@@ is a continuous loop in that plane. In fact, it is the loop that starts at @@2@@ and encircles the origin once counterclockwise. But if @@\gamma@@ is contractible to a point, then @@f \circ \gamma@@ is as well — indeed, a small adjustment to the input loop gives a small change to the output loop. But it's known that continuously contracting a loop encircling the origin down to a point is impossible. □

Corollary: The image @@\mathcal{V}(\Conf{\CC}{n})@@ is not simply connected.

From above, consider @@\mathcal{V} \circ \gamma@@. By assumption, the resulting loop is contractible to a point, so all of the preimages of that loop can also be contracted; this comes from the homotopy lifting property. But the argument above shows that can't happen in this case. □

---

I think I'm gonna end things off here. This was an interesting rabbit hole to dive down. I've never had any formal training in topology or even analysis; I studied to be a computer scientist, after all. Still, I think I learned a good deal by trying to understand statements made in the languages of those areas. Either way, I think I'd have an easier time picking them up if I have to in the future.